Quisiera enlazar este post con el realizado por Gladys en este blog titulado «Qué es Cpk?«. Concretamente voy a adentrarme en una de las fuentes de error anunciado en ese post a propósito del tamaño de la muestra.
¿Alguno de Uds. se ha encontrado en ocasiones que, ante el requisito de su cliente de Cpk ≥ 1,33, ha tenido que establecer un plan de acción que ha llevado a mejoras de utillajes, métodos, nuevas mediciones, etc. cuando en la homologación le ha dado un Cpk inferior en algunas de las cotas? Antes de seguir adelante déjenme recordarles unas cuestiones básicas de estadística
- Si el Cpk se ha calculado sobre una muestra de la población, todas las conclusiones serán estimaciones.
- Si admitimos la estimación, hay que hablar del porcentaje de error de la misma o su complementario el nivel de confianza, cosa que rara vez aparece en los requisitos del cliente
- Cuanto más pequeño es el muestreo, más error hay en la estimación.
- El cálculo del Cpk se basa en que la producción sigue una ley normal.

Pongamos ahora un ejemplo muy habitual:
- Hemos realizado un muestreo sobre 50 piezas (nº muy típico en la práctica del Cpk)
- Hemos calculado un Cpk = 1,27
¿Nos mandarán al infierno con rechazo de la homologación, el plan de acciones, nuevas muestras, nuevos informes, etc., etc.? ¿O seremos nosotros los que propondremos un retraso en la entrega de muestras hasta que arreglemos nuestra cocina? (La 3ª opción no me la leerán aquí)
Antes de darles una solución hagamos esta reflexión:
Si suponemos un nivel de confianza del 98% (ya que estamos en plena vorágine de los ppm’s, cero defectos, etc.) entonces nuestra situación es
”Basándome en un muestreo de 50 piezas, tengo el 98% de probabilidades de que el Cpk esté entre 0,95 y 1,59”
Total, que tenemos la misma probabilidad de tener un proceso “podrido” (0,95) que de tener un proceso “de película” (1,59).
Si tenemos un poco más de “manga ancha” y admitimos un nivel de confianza del 90% pues no mejoramos mucho nuestra situación ya que entonces puedo decir que con ese nivel de confianza tengo la misma probabilidad de tener un Cpk de 1,03 que 1,45.
SOLUCIÓN: merece la pena aumentar el tamaño de la muestra y, con ayuda de un software como MINITAB, ver la evolución del Cpk y su nivel inferior para un nivel de confianza determinado. Les dejo un ejemplo de dicha evolución usando el citado software. Los resultados que aparecen en las gráficas siguientes pertenecen a muestras tomadas de una misma población.
Muestra de 50 piezas. Cpk 1,27. Lower CL 0,95. Upper CL 1,59.
Muestra de 100 piezas. Cpk 1,52. Lower CL 1,25. Upper CL 1,78.
Muestra de 150 piezas. Cpk 1,53. Lower CL 1,32. Upper CL 1,75.
Muestra de 200 piezas. Cpk 1,52. Lower CL 1,34. Upper CL 1,71.
Conclusiones:
- Una muestra mayor me dará una mayor probabilidad de que los resultados calculados se acerquen a los que obtendría-mos si hubiésemos medido toda la población.
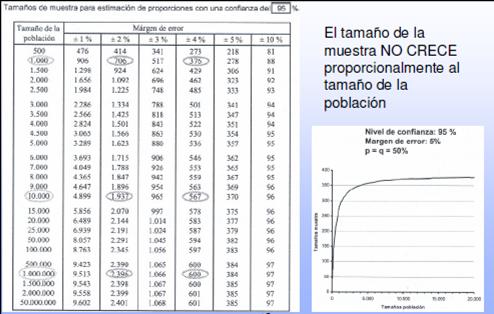
- El tamaño de la muestra no crece proporcionalmente con el tamaño de la población (ver ejemplo en tabla siguiente). Vemos en el ejemplo expuesto que entre una muestra de 150 piezas y una de 200 piezas hay poca diferencia en los resultados.
Más adelante, en otro artículo, complicaremos la reflexión para el caso de un proceso que no sigue una distribución normal.
